V laboratoři kvantových výpočtů spojujeme inovaci
a spolupráci, abychom formovali budoucnost kvantové technologie. Nacházíme se v čele výzkumu kvantového počítání a naše laboratoř je zasvěcená prohlubování teoretického porozumění, vývoji praktických aplikací a podpoře partnerství mezi akademickým světem
a průmyslem. Specializujeme se na oblasti jako řešení problémů optimalizace, kvantové strojové učení, kvantová faktorizace a optimalizace kvantových obvodů, kvantová korekce chyb. Nabízíme vzdělávací aktivity, které zajistí, že znalosti a odbornost budou sdíleny a rozvíjeny mezi novými generacemi kvantových vědců a inženýrů.
Portfolio
Řešení optimalizačních úloh pomocí QAOA
Quantum Approximate Optimization Algorithm (QAOA) je dalším typem VQA a stejně jako VQE hledá nejmenší vlastní číslo, nicméně
v tomto případě je důležitější hodnota stavového vektoru, který tomuto nejmenšímu vlastnímu číslu odpovídá. Tento (vlastní) vektor by pak měl být řešením optimalizační úlohy, zakódované v použitém operátoru. Oblast použití tohoto algoritmu je omezena pouze tím, zda je možné daný optimalizační problém do takového operátoru zakódovat. Lze jej tedy použít pro širokou škálu kombinatorických optimalizačních problémů, jako jsou problém batohu, rozdělení grafů, řazení úloh, problém obchodního cestujícího a podobných. Ještě zajímavější jsou možnosti použití QAOA ve finančnictví (optimalizace portfolia), v energetice (zvýšení odolnosti rozvodné sítě), v komunikaci (detekce přenášených binárních symbolů),
v biochemii (skládání proteinů), v počítačovém vidění (detekce objektů), ve strojovém učení (trénování modelů) a v dalších.
Provádíme experimenty s nastavením tohoto algoritmu, abychom dosáhli přesnější a rychlejší konvergence při přibližování se
ke správnému řešení úlohy.
Kvantové strojové učení
Kvantové strojové učení je výzkumná a inženýrská oblast, která zkoumá souhru jevů kvantové mechaniky a strojového učení. Takové vnitřní rysy kvantové mechaniky, jako je linearita, náhodnost, superpozice a provázanost, lze přirozeně využít ke zpracování dat pomocí kvantových zdrojů. Mnoho klasických technik strojového učení využívá lineární algebru a teorii pravděpodobnosti jako své základy, proto existuje přirozené mapování mezi matematickou teorií strojového učení a dvěma prvními rysy kvantové mechaniky. Přesto tyto dva poslední jevy otevírají dveře nové éře výpočetního výkonu
a umožňují nám řešit výzvy, které byly dříve příliš složité nebo časově náročné.
- Vytvoření certifikace a učení technik pro kvantové operace
- Vytváření nových metod ověřování a benchmarkingu NISQ architektur
- Použití kvantových sítí ke kvantovým algoritmům
- Rozvoj teorie kauzální struktury
Kvantová faktorizace poloprvočísel
Exponenciální výpočetní náročnost faktorizace velkých poloprvočísel je základem bezpečnosti RSA – nejrozšířenějšího současného kryptosystému, používaného pro bezpečný přenos dat. Nejlepší současné faktorizační algoritmy, programovatelné na klasických počítačích, mají sub-exponenciální složitost. Pro úspěšnou faktorizaci RSA klíče dlouhého 2048 bitů (v současnosti doporučovaná a nejpoužívanější délka) by dnešní superpočítače potřebovaly řádově miliardy let. Pro bezpečnost celosvětového přenosu dat je tedy zcela zásadní vědět, že ani kvantové počítače takto dlouhý klíč nedokážou v rozumném čase faktorizovat a tím se dostat k přenášeným informacím.
V zásadě existují dvě cesty, jak pomocí kvantového počítače poloprvočísla faktorizovat. První je pomocí známého Shorova algoritmu, jehož použití ovšem ztěžuje potřebnost kvantové implementace modulárně exponenciální funkce. Proto se tímto algoritmem zatím podařilo faktorizovat na kvantovém počítači pouze číslo 21 a při pokusu o faktorizaci čísla 35 byly naměřeny nejednoznačné výsledky. Cílem našeho snažení v této oblasti je úspěšná faktorizace daleko větších čísel pomocí tohoto algoritmu.
Druhou cestou je převedení faktorizačního problému na problém optimalizační. Ten se pak dá vyřešit pomocí kvantového žíhání nebo adiabatického kvantového počítání, ze kterého vychází i výše zmíněný QAOA. Tímto způsobem byla faktorizována daleko větší čísla (zatím největší je 1,099,551,473,989), ale úspěch těchto faktorizací byl hodně závislý na klasických výpočtech, aby došlo ke snížení počtu potřebných qubitů. V rámci řešení optimalizačních problémů pomocí QAOA se rovněž zabýváme tímto způsobem faktorizace.
Optimalizace kvantových obvodů
Optimalizace kvantových obvodů je důležitý proces, jehož cílem je zvýšit účinnost a výkon kvantových algoritmů minimalizací zdrojů potřebných k jejich provedení. V oblasti kvantových počítačů, kde jsou qubity základními jednotkami výpočtu, se optimalizace kvantových obvodů stává klíčovou kvůli přirozené nestabilitě
a omezené koherenční době qubitů. Tato optimalizace zahrnuje různé techniky, jako je sloučení hradel, zrušení hradla a přeskupení qubitů, všechny zaměřené na snížení počtu hradel, hloubky nebo jiných metrik při zachování funkčnosti obvodu. Zefektivněním kvantových obvodů mohou výzkumníci zmírnit chyby, zlepšit škálovatelnost a připravit cestu pro realizaci praktických kvantových algoritmů schopných efektivně řešit složité výpočetní problémy. Optimalizace kvantových obvodů navíc hraje klíčovou roli při překlenutí propasti mezi teoretickými algoritmy a jejich reálnými implementacemi na kvantovém hardwaru, čímž posouvá oblast kvantových počítání směrem k dosažení jeho plného potenciálu.
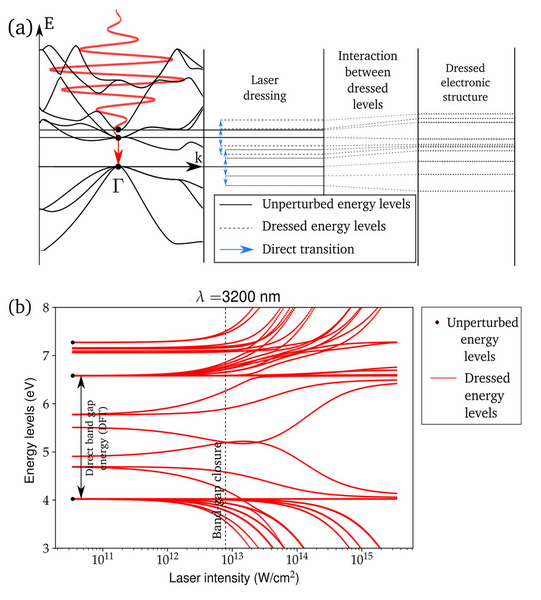
Skupina Kvantové dynamiky struktur vyvíjí řadu prediktivních simulačních metod v oblasti deep-tech (např. fotonika, polaritonika, chemická fyzika, spektroskopie), a to jak na klasické, tak na kvantové úrovni. S podporou simulačních nástrojů kvantové molekulové dynamiky ("ab-initio" metoda výpočtu těsné vazby na bázi funkcionálu hustoty, DFTB, časově závislá teorie elektronové hustoty, TDDFT) a nástrojů pro predikce v kvantové i klasické polaritonice, skupina nabízí předpovědi a nejnovější poznatky pro urychlení objevů a vyhovění potřebám v různých oblastech vědy a technologií. Oblasti uplatnění skupiny zahrnují návrh fyzických qubitů pro přípravu budoucích kvantových počítačů s využitím poznatků získaných při zkoumání dynamiky různých struktur (světlo, hmota, kvazičástice), které se vyskytují v řadě systémů ve fyzice, chemii, spektroskopii a dalších oblastech.
Kvantová komunikace využívá principy kvantové mechaniky
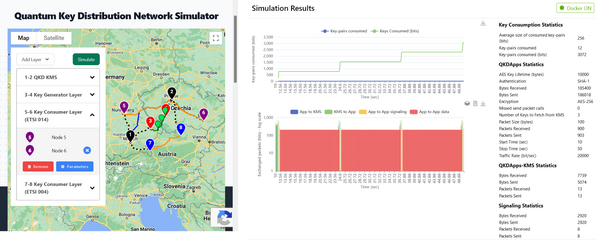
k bezpečnému přenosu dat a ke kódování informací využívá kvantové bity (qubity). Jednou z hlavních výhod kvantové komunikace je možnost dosáhnout teoreticky neprolomitelného šifrování prostřednictvím kvantové distribuce klíčů (QKD), což zajišťuje integritu a důvěrnost dat. Výstupy dosažené naším výzkumným týmem jsou spjaty s dokončenými projekty OpenQKD a NATO Quantum5 financované z programu H2020. Cílem projektu OpenQKD bylo pokročit ve vývoji a implementaci kvantových sítí pro distribuci klíčů (Quantum Key Distribution, QKD) v celé Evropě a zvýšit tak bezpečnost přenosu dat. Projekt NATO Quantum5 přispěl k bezpečnosti přenosu informací v 5G sítích v univerzitních kampusech a to implementací kvantové kryptografie v 5G komunikaci. Tým dokáže provádět simulace QKD sítí a implementaci protokolů, šifrovacích nástrojů a nových metod v kvantové komunikaci. Značnou výhodou je skutečnost, že tým již řadu let vyvíjí open-source QKD simulátor QKDNetSIM a může do simulátoru implementovat nová řešení a ověřovat jejich platnost.
Kvantová korekce chyb
Kvantová korekce chyb (QEC) je sofistikovaný proces kódování a dekódování, jehož cílem je chránit kvantovou informaci před rušivými vlivy kvantového šumu. QEC je klíčovou součástí vývoje plně funkčních kvantových počítačů. Zásadní průlom v této oblasti přinesl Shorův kód, který jako první umožnil kódování jednoho logického qubitu do devíti fyzických qubitů, čímž položil základy moderní kvantové korekce chyb. Různé metody korekce se liší typy šumu, které dokážou eliminovat, přičemž většina se opírá o Knill-Laflammovu větu. Pokud jsou splněny její podmínky, příjemce může vytvořit dekódovací schéma umožňující obnovu původní informace. Kvantová korekce chyb se postupně rozvíjela s inspirací z klasických metod. Mezi významné přístupy patří Calderbank-Shor-Steane (CSS) kódy, kvantové Reed-Solomonovy kódy a stabilizátorové QEC kódy. Současný výzkum se zaměřuje na inovativní techniky, jako jsou entanglement-assisted error-correcting codes, které využívají sdílené kvantové provázání ke zvýšení efektivity korekce chyb. S tím, jak se pole kvantové korekce chyb vyvíjí, se sen o plně odolném kvantovém počítání postupně stává realitou.